25 ++ odds versus probability 164252-Are odds and probability the same

 Odds can be expressed as a ratio of the probability an event will happen divided by the probability an event won't happen Odds in favor of A = A / (1 A), usually simplified to lowest terms, For instance, if the probability of an event occurring is 075, then the odds for it happening are 075/025 = 3/1 = 3 to 1 for, while the probability that it doesn't occur is 1 to 3 againstIn the lower, I varied the values of the p parameter The probability distribution function isConverting fractional odds to implied probability To calculate the implied probability from fractional odds the equation is denominator / (denominator numerator) * 100 = implied probability Therefore to find out the probability of a Murray win would simply be 2 / (2 9) * 100 = 181% As you can see this is the same probability as with

Voters Are Starting To Doubt Trump S Reelection Chances Fivethirtyeight

Are odds and probability the same

Are odds and probability the same- Odds are expressed in several ways (see below), and sometimes the term is used incorrectly to mean simply the probability of an event Conventionally, gambling odds are expressed in the form "X to Y", where X and Y are numbers, and it is implied that the odds are odds against the event on which the gambler is considering wageringGambling Odds Versus Probabilities In gambling, the odds on display do not represent the true chances that the event will occur, but are the amounts that the bookmaker will pay out on winning betsIn formulating his odds to display the bookmaker will have included a profit margin which effectively means that the payout to a successful bettor is less than that represented by the true chance

Compound Probability Definition

 Odds versus probability 27 July 11 By John Robison I absolutely love your column and answers to all our questions It's nice to know there is someone who tells it like it is with no jive one way or the other I would like to know your thoughts on possibility (the odds) vs probability You tell people, rightfully so,4 rows  The primary difference between odds and probability is that while odds is a ratio ofEach outcome of an experiment or a collection of outcomes make an event If each outcome of an experiment has an equal chance of occurrence then these outcomes are equally likely As in the example of rolling a die the chances of occurrence of numbers among 1 to 6 are equally likely Probability Formula

 Converting Odds to Probability Simply add the 2 components of the odds together to make a new denominator, and use the old numerator eg If the odds are 35, or 3 to 5, the probability is 3 ÷ (35) = 3/8 = 375% Converting Probability to Odds Take the probability, and divide it by its compliment = (1itself) eg Convert betting odds to probability Now we want to see what those odds mean in terms of probability There is another simple formula that takes the numbers in a Probability to Odds Calculator More about the Probability to Odds Calculator so that you can better understand the elements used in this calculator It is common0609 Odds versus Probability Odds is less intuitive than probability Even though these terms are often used interchangeably, there is a marked difference between the two Keith McNulty notes in his article titled, "Are you mixing up odds with probability?" that both terms "imply an estimate of chance" Even though these terms are related concepts, they are notably different in "scale and meaning"

 Chance and Probability Definition and Example Problems Read More Chance is the occurrence of events in the absence of any obvious intention or cause It is, simply, the possibility of something happening When the chance is defined in mathematics, it is called probability Odds can be helpful when we want to compare how much larger one probability is relative to another An event with a probability 75% has odds of 75 to 25 We can simplify this to 3 to 1 This means that the event is three times more likely to occur than not occur Cite this ArticleOdds and probability can be expressed in prose via the prepositions to and in "odds of so many to so many on (or against) some event" refers to odds – the ratio of numbers of (equally likely) outcomes in favor and against (or vice versa);

The Odds Of Success Chances Of You Making It Big

2

Odds The odds in favor of an event is the ratio of the number of ways the outcome can occur to the number of ways the outcome cannot occur # of ways the event CAN occur # of ways the event CANNOT occur This is actually a lot easier than probabilityIt is obvious that the probability of such a numerically ordered arrangement decreases rapidly as the number of components increases For any linear system of 100 components in specified order, the probability is one in 100!, or one chance in 10 158 (a Odds of dying estimates assume that mortality trends change slowly over time with changes of only a few percentage points from year to year Currently, COVID19 trends are changing too rapidly to confidently anticipate future risk levels Visit the Injury Facts COVID19 page to track realtime data in the United States COVID19

Compound Probability Definition

2

When comparing two events, it common to phrase probability statements in terms of odds De nitionThe odds of event E versus event E0 are the ratio of their probabilities P(E)=P(E0) If unspeci ed, the second event is assumed to be the complement Ec So the odds of E are P(E) O(E) = P(E c) For example, O(rain) = 2 means that the probability Binomial So I think that the reason you see lots of RR, but very little PR is that PR is constructed from probability/Binomial type quantities, while RR is constructed from rate type quantities In particular note that incidence can exceed 100% if people can catch the disease multiple times per year, but probability can never exceed 100%How to find probability and odds and the difference between the two We also discuss experimental probablility, theoretical probability, odds in favor, and

How To Find The Probability Of An Event And Calculate Odds Permutations And Combinations Owlcation

Statistical Analysis Of Nba Odds How To Not Lose Money Betting On Basketball By Tomas Kristijonas Uzdavinys Medium

 Odds are just a way of stating a probability That's just a mathematical way of looking at how likely it is that something is going to happen All probabilities are ratios between eventsThe Ask Dr Math forum has several entries on odds versus probability Summarizing, one way to conceptualize (nontechnically) the probability of an event is the number of ways that an eventGambling Odds Versus Probabilities In gambling, the odds on display do not represent the true chances that the event will occur, but are the amounts that the bookmaker will pay out on winning bets In formulating his odds to display the bookmaker will have included a profit margin which effectively means that the payout to a successful bettor is less than that represented by the true chance Which means that probability and odds do not mean the same thing (although we can convert from one to the other) Without going into too much detail, probability is a number between 0 and 1 that tells you the fractional likelihood that something will happen

What Is The Difference Between Logit And Probit Models

2

 Math odds versus gambling odds As far as I remember the mathematical concept odds is defined as the probability something is true divided by the probability that it is not the ratio of the probability that the event will happen to the probability that the event will not happen However, reading about odds in sports gambling, Wikipedia says this Odds, on the other hand, are the ratio of favorable outcomes to unfavorable outcomes The denominator contains ONLY the marbles that aren't the favorable outcomes Odds uses the contexts of good outcomes and bad outcomes Written as fractions, these two values are completely different Probability is 1/4 while odds in favor are 1/3Similarly, the probability that a single roll of the die will be a 1 is 1/6 The same holds true for 2, and for 3, and for 5, and for 6 The singleevent probability that a roll of the die will result in any one face you select is 1 in 6 Cumulative Probability Cumulative probability measures the odds of two, three, or more events happening

Using Bayes Rule In Diagnostic Testing A Graphical Explanation

Pdf Common Pitfalls In Statistical Analysis Odds Versus Risk

 Odds, on the other hand, are a measure of chance that cannot be mathematically calculated, per se The odds of a particular event occurring is more a measure of chances for the event happening to the chances of the occurrence not happening –that is, (chances for)To convert odds to probability, take the player's chance of winning, use it as the numerator and divide by the total number of chances, both winning and losing For example, if the odds are 4 to 1, the probability equals 1 / (1 4) = 1/5 or % Odds of 1 to 1 (50%) are called "evens," and a payout of 1 to 1 is called "even money" The odds are defined as the probability that the event will occur divided by the probability that the event will not occur A probability of 0 is the same as odds of 0 Probabilities between 0 and 05 equal odds less than 10 A probability of 05 is the same as odds of 10 Think of it this way The probability of flipping a coin to heads is 50%

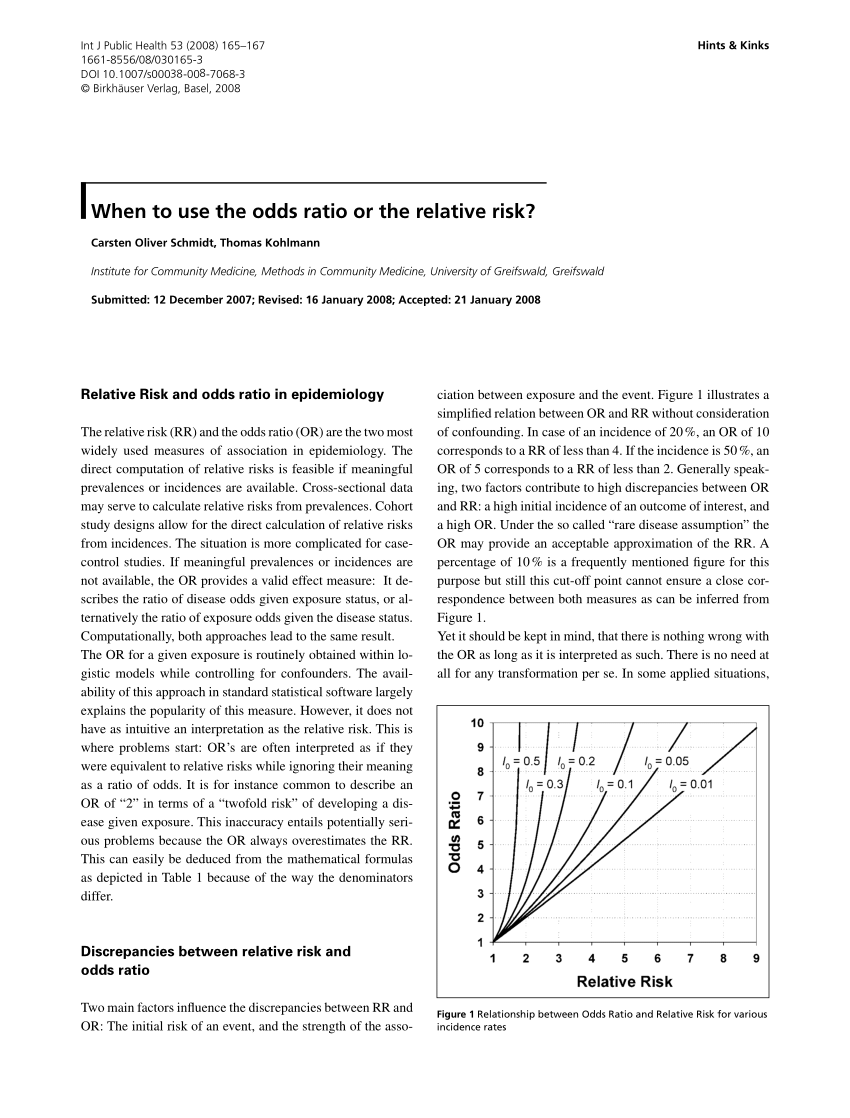
Pdf When To Use The Odds Ratio Or The Relative Risk

The Bounded Rationality Of Probability Distortion Pnas

Of Baer, Grabb, and Johnston's (1990) interpretation of odds ratios is well taken However (continuing with the Baer, Grabb, & Johnston 1990 example), if the odds ratio (for the odds of having "no say" in government) for English Canadians versus Americans is 1345, then it is correct to say that the odds of The basic difference is that the odds ratio is a ratio of two odds (yep, it's that obvious) whereas the relative risk is a ratio of two probabilities (The relative risk is also called the risk ratio) Let's look at an example Relative Risk/Risk Ratio Suppose you have a school that wants to test out a new tutoring program • Chance is an everyday word used in a situation where we are talking about an event taking place whereas probability is a precise measurement of that chance • Probability is a special branch of mathematics that helps people decide the percentage of likelihood of an event taking place whereas chances of an event taking place in daily life are merely opinions

Frequentist Statistics Ppt Download

How To Read Odds 13 Steps With Pictures Wikihow

 Probability is the measurement of the likelihood of an event's occurrence The value is expressed between 0 and 1, where 0 indicates impossibility, and 1 means certainty So when the value is between 0 and 1, we usually expressed this in decimal terms As the word probability sounds a bit too technical, some writers prefer to use a simpler wordI show you how to find / write probability, odds in favor and odds against About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How worksA probability, on the other hand, is a measure or estimation of how likely is it that an event will come to pass, or that a statement is true Probabilities are given a value between 0 or 1, where 0 is a 0% chance of the event happening, ie it will not happened, and 1 is a 100% chance

Odds Ratios And Risk Ratios Youtube

Odds Ratio The Odds Ratio Is Used To Find The By Analyttica Datalab Medium

Odds, are given as (chances for success) (chances against success) or vice versa If odds are stated as an A to B chance of winning then the probability of winning is given as P W = A / (A B) while the probability of losing is given as P L = B / (A B) For example, you win a game if you pull an ace out of a full deck of 52 cardsThis article takes issue with propositions tendered in Roncek (1991) regarding the definitions of odds and odds ratios, the interpretation of the partial slope, and an emphasis on using predicted probabilities to convey the impact of categorical predictors in logit analysis This article correctly defines odds and odds ratios, provides the correct interpretation of the partial slope, and Odds Is Related to Probability The formal way to describe the odds is as the probability of the event divided by the probability of the nonevent So odds are the ratio of two fractions the number of events divided by the number of subjects (the probability of the event) and

Using Bayes Rule In Diagnostic Testing A Graphical Explanation

Voters Are Starting To Doubt Trump S Reelection Chances Fivethirtyeight

Odds ( female) = 7 / 3 = odds ( male) = 3 / 7 = We could use this information to compute an odds ratio O R = / = 544 Thus a female is 544 times more likely to get in But since the probability of an event is just p p q the probability of a male getting in is 30%, while the probability of a female getting Figure 1 The binomial probability distribution function, given 10 tries at p = 5 (top panel), and the binomial likelihood function, given 7 successes in 10 tries (bottom panel) Both panels were computed using the binopdf function In the upper panel, I varied the possible results;"chances of so many outcomes, in so many outcomes" refers to probability – the number of (equally like) outcomes in favour relative to the

Logistic Probability Score The Logistic Probability Score Function By Analyttica Datalab Medium

Ppt Main Points To Be Covered Powerpoint Presentation Free Download Id

Odds are ratios, specifically, ratios of probabilities The units of the odds of an event A (a ratio) are expressed in orders of magnitude relative to event A not occurring Orders of magnitude are not strictly confined to the continuum of the real line in the interval 0,1 Therefore, the scaling of probability, chances and odds are not the same Decimal odds are a simple reflection of the return you will receive for each single unit placed In other words, odds of 165 means that for every 100 you place on a particular outcome, you will receive a profit of 065 should that outcome prevail To convert these odds to their respective implied probabilities we make a simple calculation

Ncaa Com

2

How Sharp Are Bookmakers

Predicting The Future With Bayes Theorem

Relative Risk Wikipedia

Pseudorandomness When The Odds Are Against You Ppt Download

Base Rate Fallacy Biases Heuristics The Decision Lab

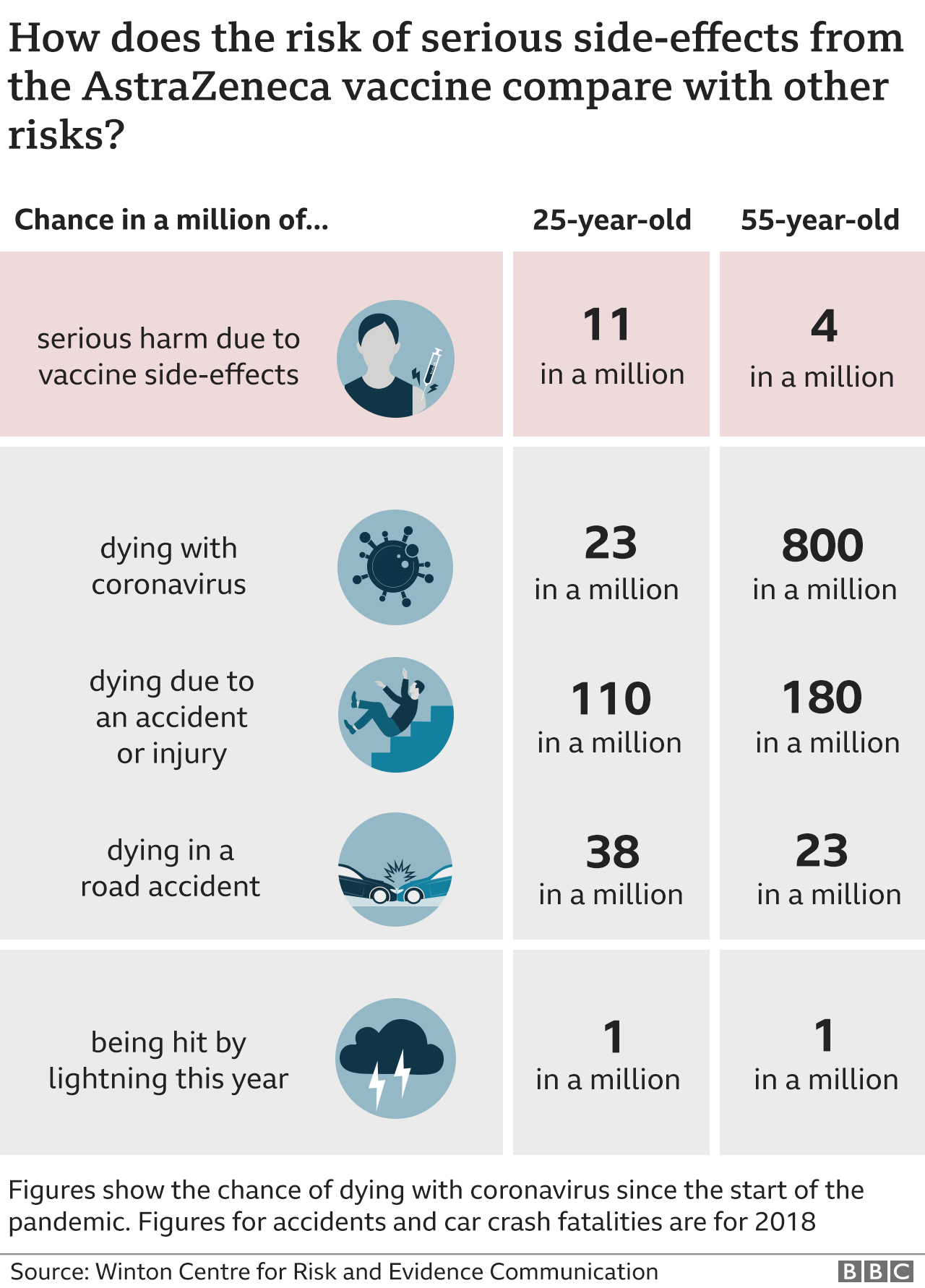
Astrazeneca Vaccine How Do You Weigh Up The Risks And Benefits c News

Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science

Calculating The Odds Of An Event Mathematics For The Liberal Arts

What Are Fraternal Dizygotic Twins

Showing The Probability Of Highly Unlikely Events Versus Winning The Lottery

Demystifying The P Value

2

Cureus What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios

Epidemiology Mph 531 Analytic Epidemiology Ppt Download

March 28 Analyses Of Binary Outcomes 2 X 2 Tables Ppt Download

Odds Ratio Relative Risk

When Are The Odds Really In Your Favor Huffpost Life

Life Insurance Is No Accident Odds Of Dying At Home More Nerdwallet

Confidence Intervals For The Odds Ratio In Logistic Regression With Two Binary X S Pdf Confidence Interval Logistic Regression

Q Tbn And9gcr Ttka12jaocnx Gn3ox9ci1ggq18vcw9359i6hq2cschyusam Usqp Cau

Super Bowl Squares And Odds Of Winning Sports Illustrated

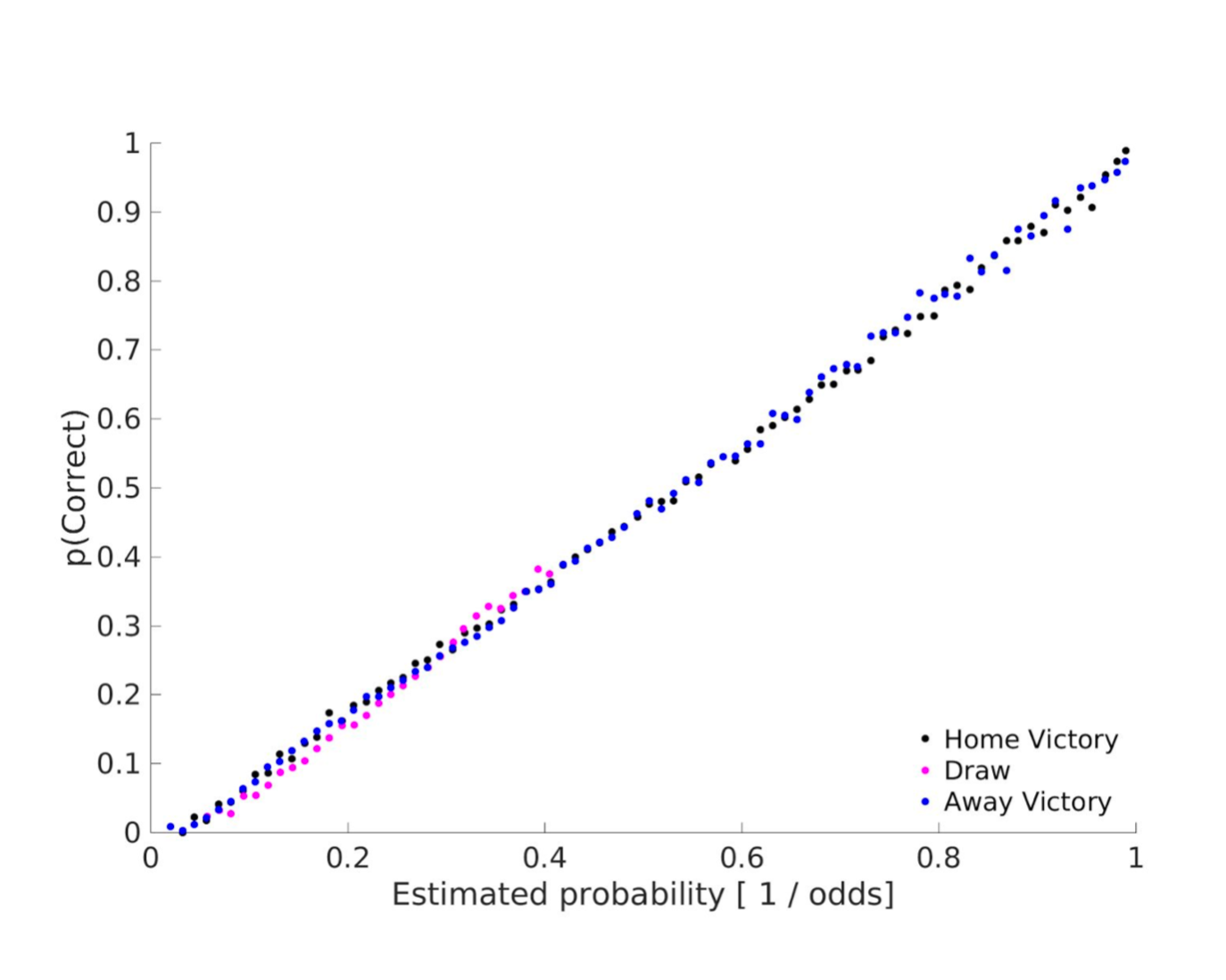
What I Ve Learnt Predicting Soccer Matches With Machine Learning Towards Data Science

Explains The Odds Of Winning The Lotto Versus Other Things That Could Happen In Life Infographic Lotto Winning Lotto

Probability Combinations 2 Of 2 Video Khan Academy

Ppt Chapter 13 Probability And Data Analysis Powerpoint Presentation Id

Probability Vs Odds In Favour Or Against An Event Examples Youtube

Mit18 05s14 Reading12b Bayesian Inference Statistical Theory

Using Bayes Rule In Diagnostic Testing A Graphical Explanation

The Proportional Odd Model Logistic Regression Analysis

Joint Probability Definition

Belgium Vs Italy Football Predictions And Betting Odds Italy To Win Crowdwisdom360

Poker Odds Calculator Odds Of Winning W Any Poker Hand

Birthday Problem Wikipedia

Esdownload Site Formulas Maths Formulas Coin Toss Probability 3

Compound Probability Definition

Log Odds Interpretation Of Logistic Regression Youtube

The Stata Blog Probability Differences And Odds Ratios Measure Conditional On Covariate Effects And Population Parameter Effects

How Are Logistic Regression Ordinary Least Squares Regression Linear Regression Related Why The Regression In Logistic By Rakshith Vasudev Towards Data Science

Odds Vs Probability Vs Chance Data Science Central

Why Most Published Research Findings Are False Chance

Craps Odds Detailed Explanation Of Craps Odds And Probabilities

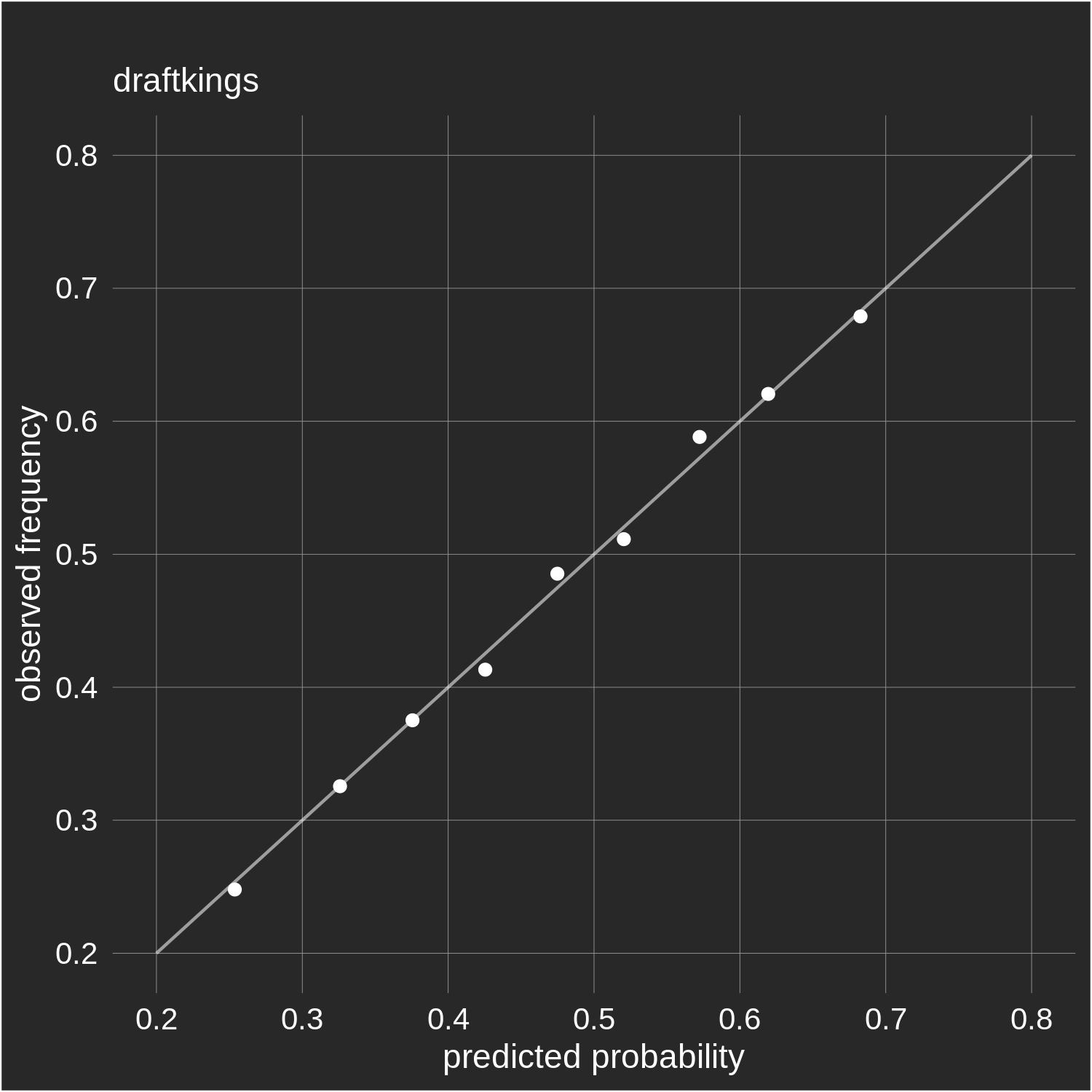
How Sharp Are Bookmakers

Ppt Main Points To Be Covered Powerpoint Presentation Free Download Id

Statquest Odds Ratios And Log Odds Ratios Clearly Explained Youtube

2

What Is An Odds Ratio And How Do I Interpret It Critical Appraisal

Q Tbn And9gctxz8owky Sul84xtk4ggzacxwhkmhguhlxwyjj9avufagdrhwm Usqp Cau

Exploring Short Deck Hold Em Part 2 Odds And Probabilities Pokernews

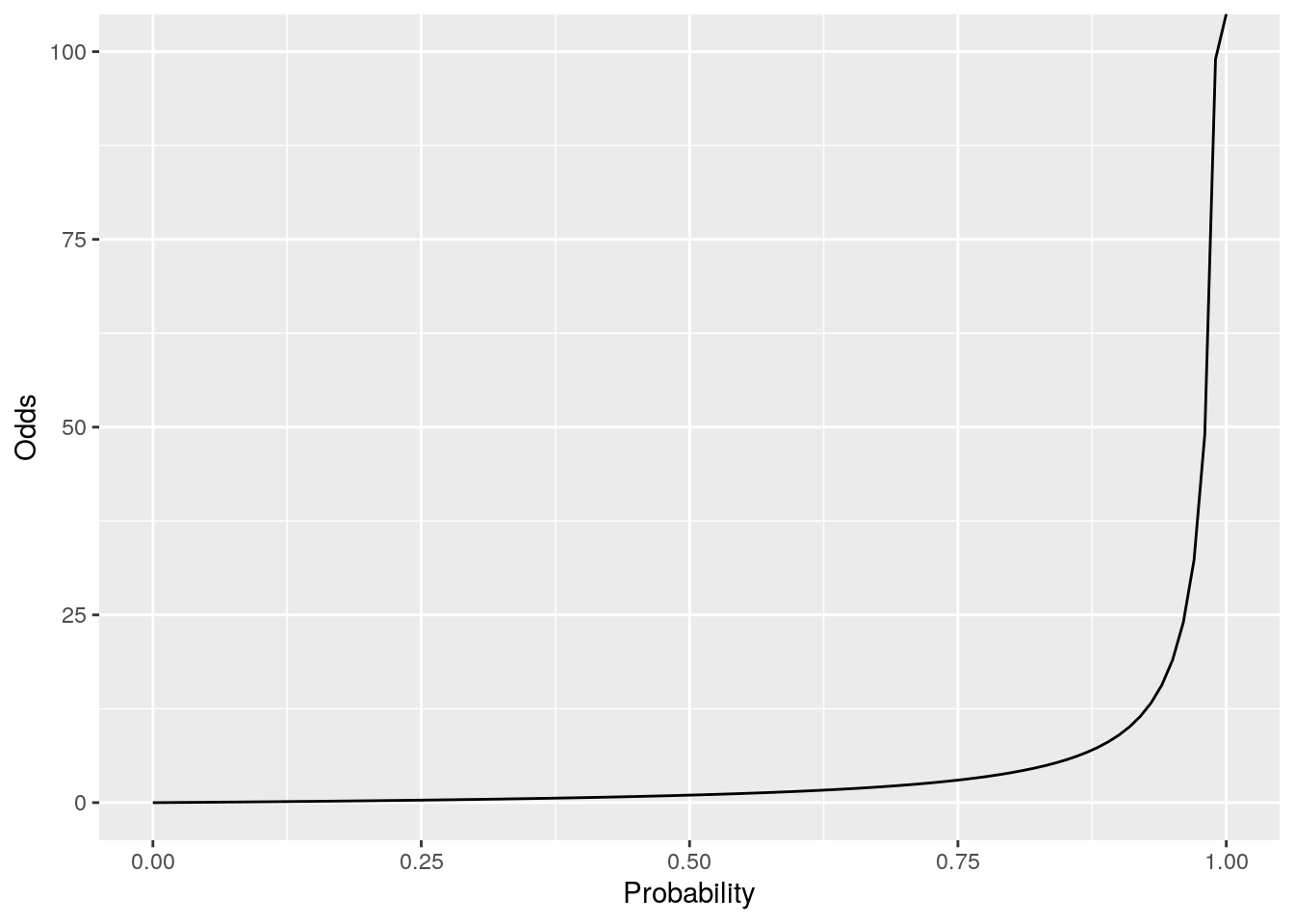
5 Binomial Logistic Regression For Binary Outcomes Handbook Of Regression Modeling In People Analytics With Examples In R Python And Julia

Probability Vs Odds Youtube

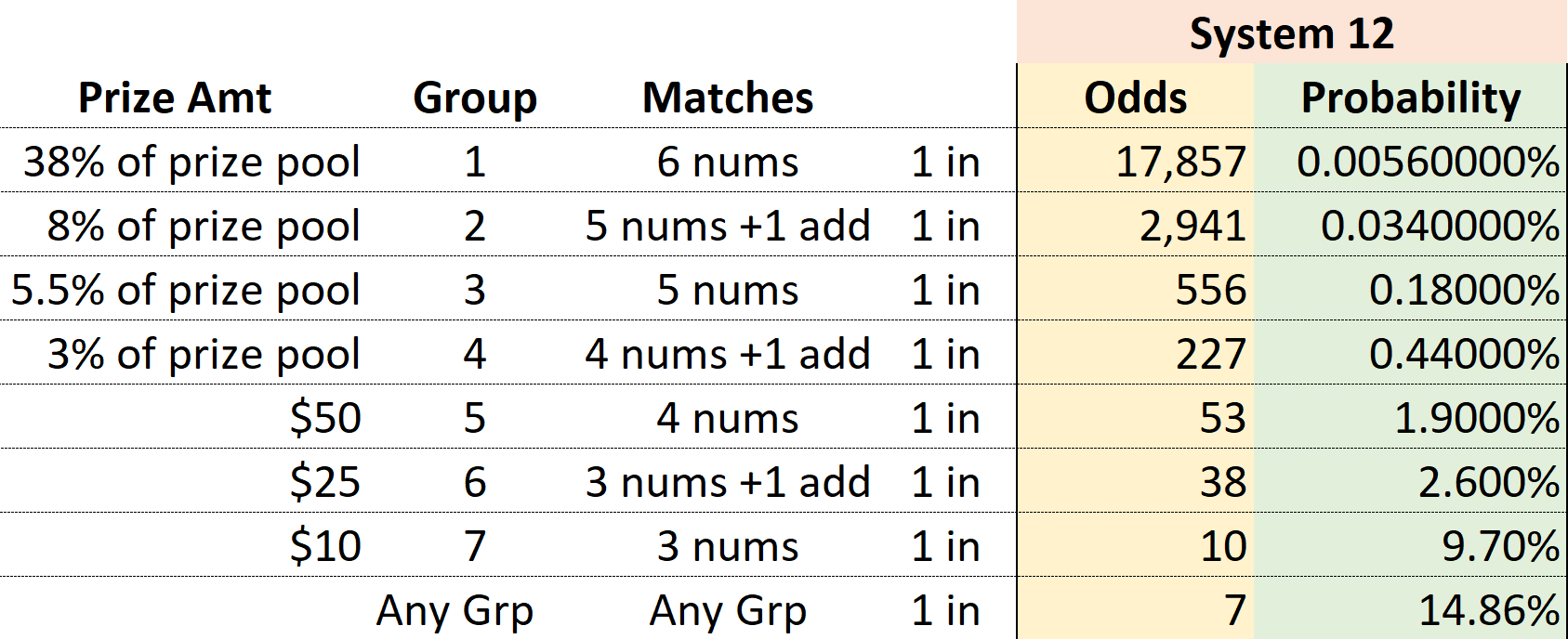
Is Itoto A Better Choice Than System 12 Theory Of Constraints

Betting Odds Explained How Are Football Odds Calculated

Odds Ppt Download

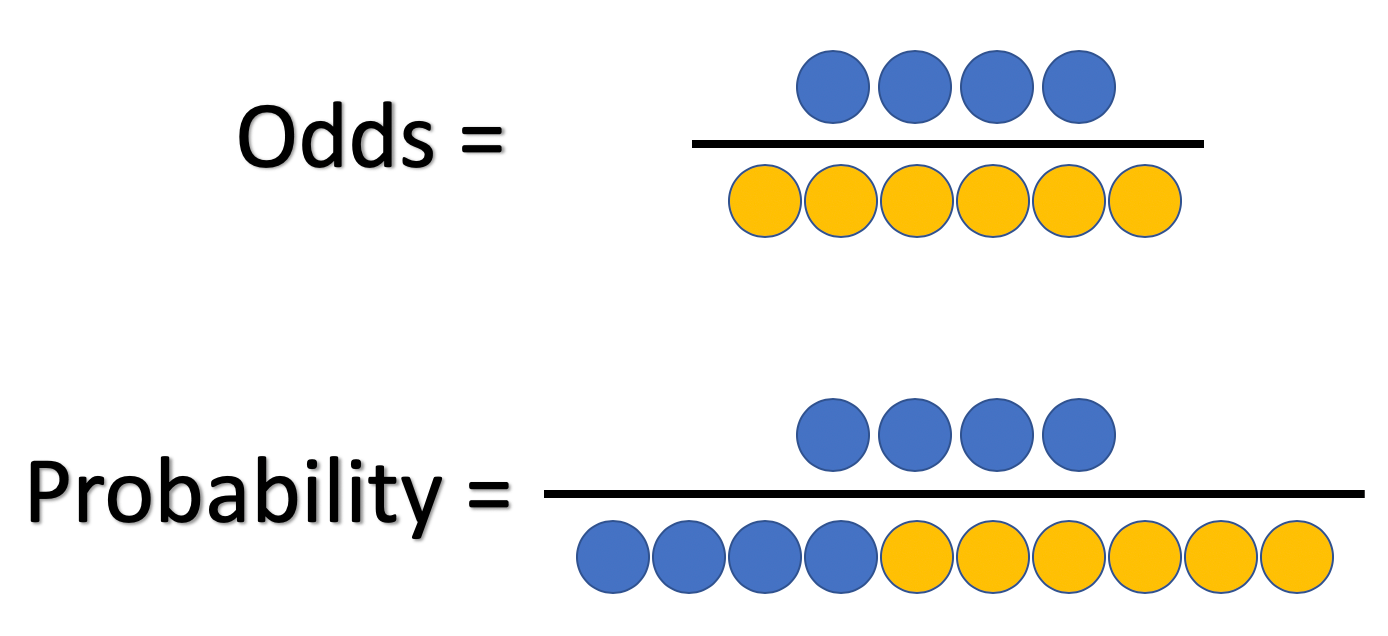
What And Why Of Log Odds What Are Log Odds And Why Are They By Piyush Agarwal Towards Data Science

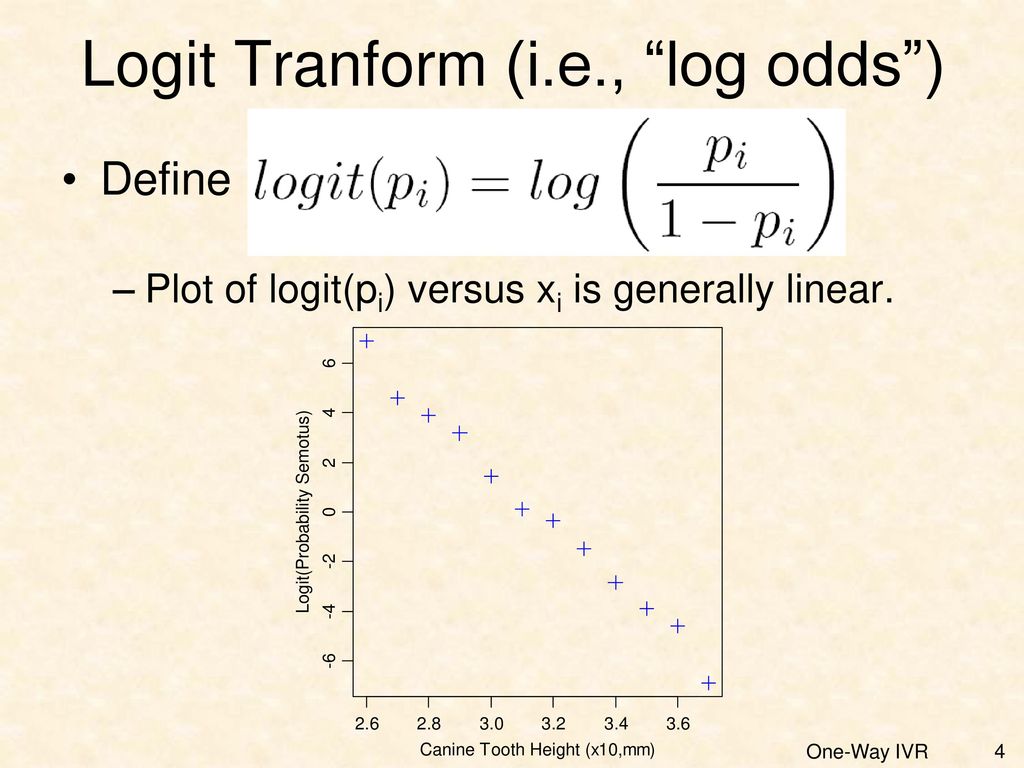
Binary Logistic Regression Ppt Download

Solved I Can T Figure Out Number 2 I Don T Know Which Fo Chegg Com

Statistics 101 Logistic Regression Probability Odds And Odds Ratio Youtube

The Bounded Rationality Of Probability Distortion Pnas

Using Bayes Rule In Diagnostic Testing A Graphical Explanation

Cureus What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios

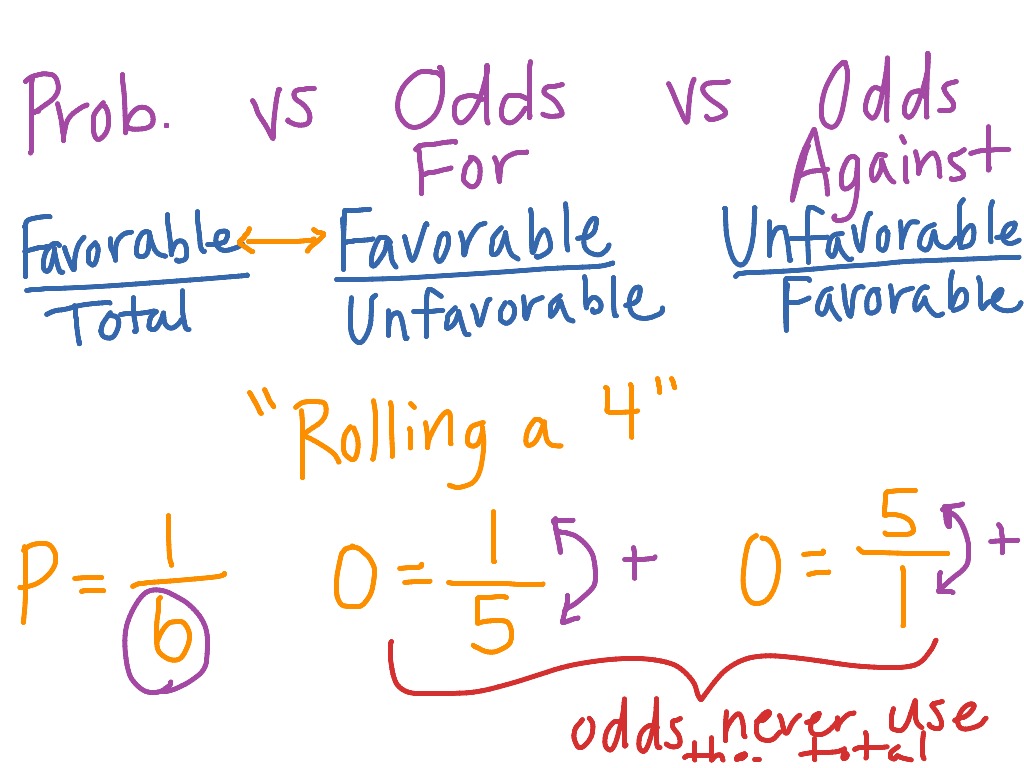
Odds Versus Probability Math Showme

Ppt Main Points To Be Covered Powerpoint Presentation Free Download Id

Monty Hall Problem Wikipedia

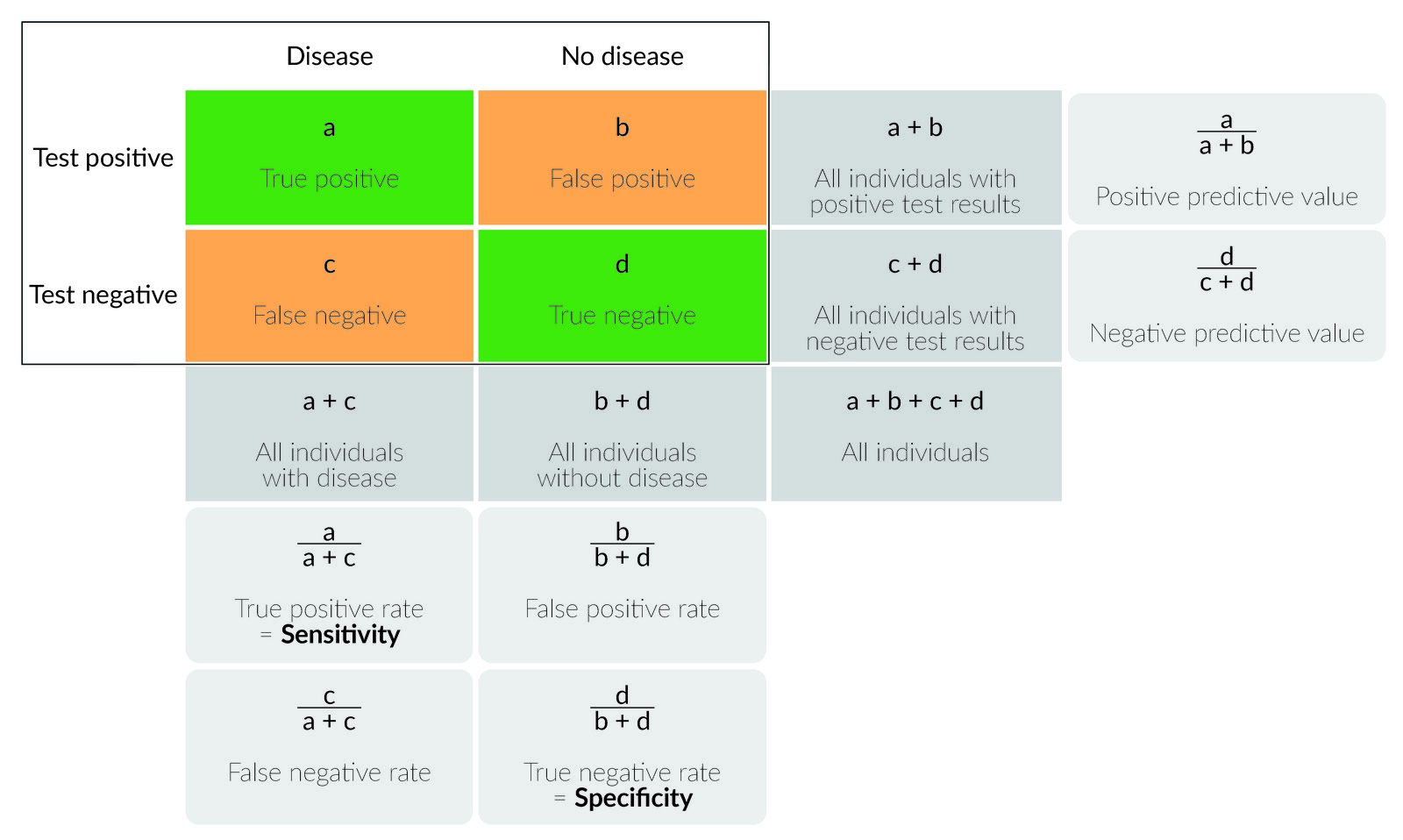
Epidemiology Knowledge Amboss

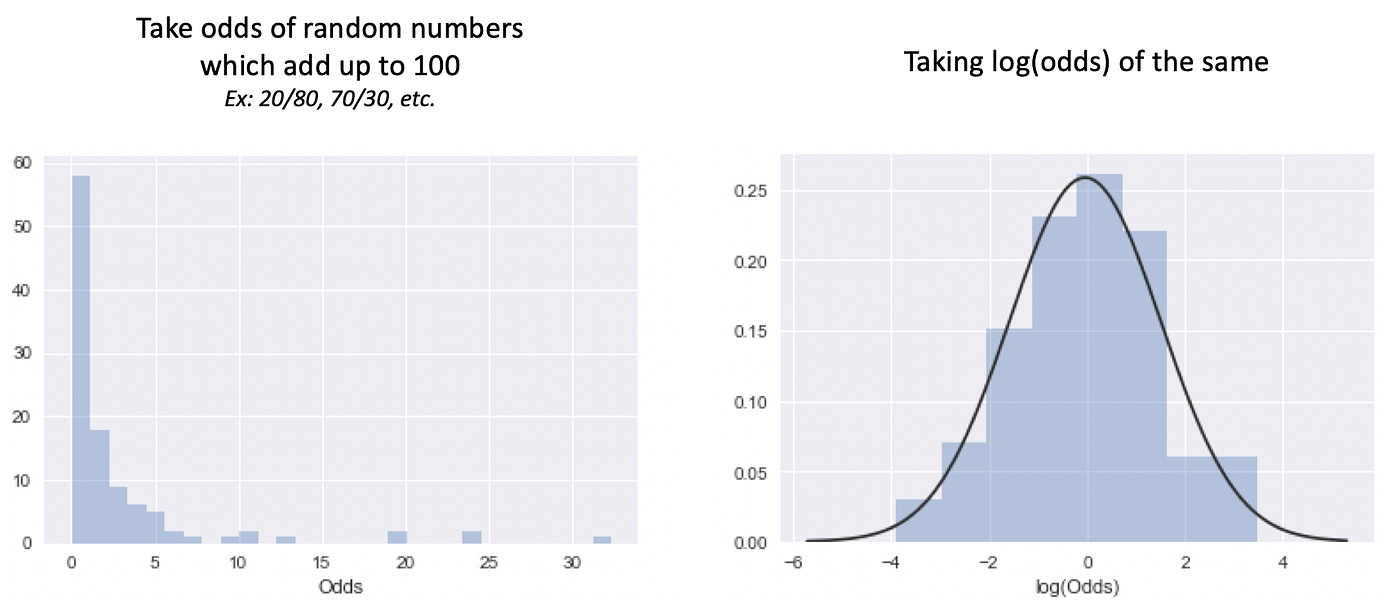
What And Why Of Log Odds What Are Log Odds And Why Are They By Piyush Agarwal Towards Data Science

The Market For English Premier League Epl Odds

The Bounded Rationality Of Probability Distortion Pnas

2

The Math Behind Betting Odds Gambling

Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science

2

Logit Wikipedia

2

Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1

Q Tbn And9gctxz8owky Sul84xtk4ggzacxwhkmhguhlxwyjj9avufagdrhwm Usqp Cau

1

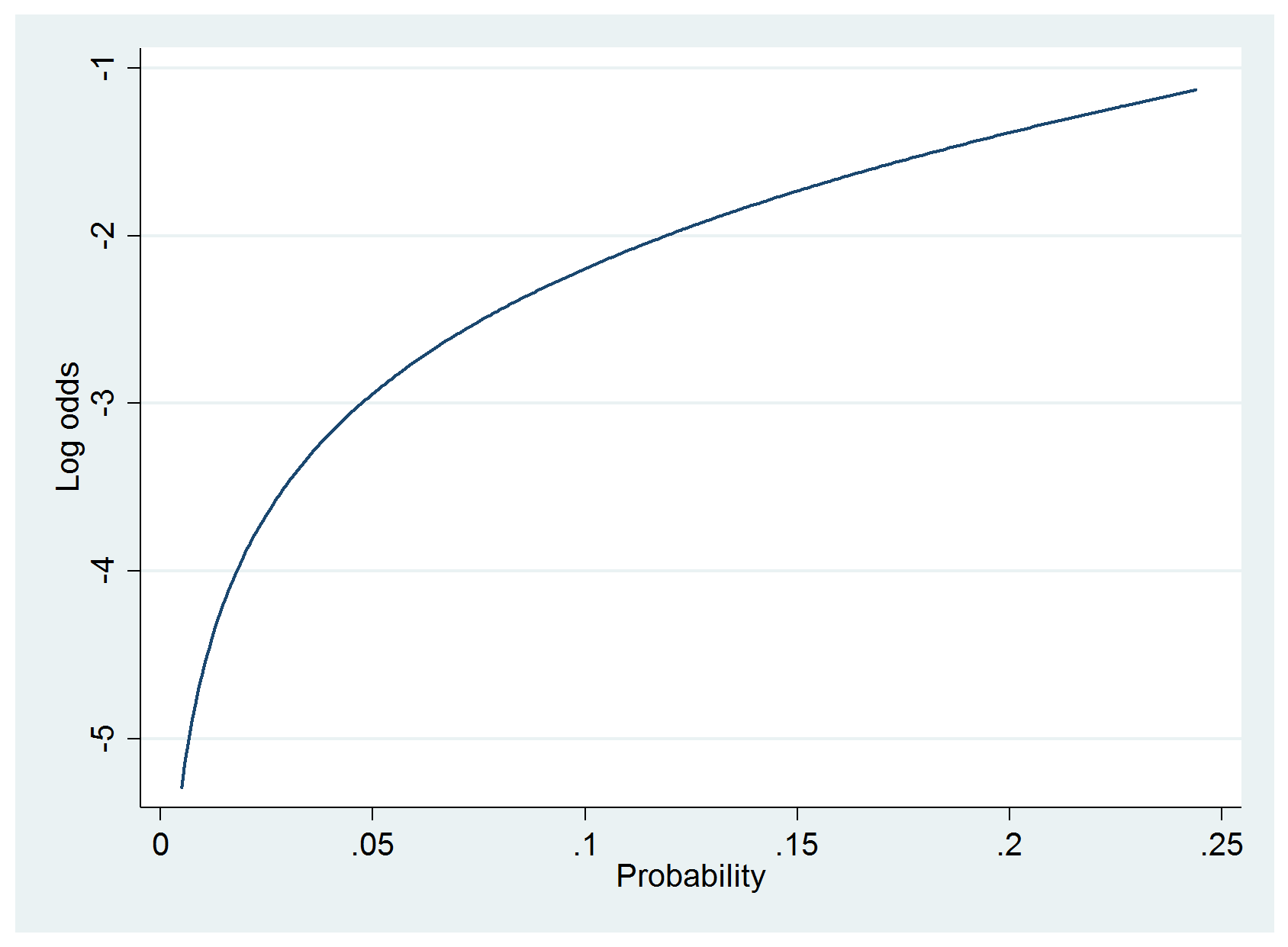
In Defense Of Logit Part 2 Statistical Horizons

What Are The Odds Of Dying From Covid 19 Vs Lightning Wqad Com

Conditional Probability Tree Diagram Example Video Khan Academy

2

Compound Probability Of Independent Events Video Khan Academy

Calculation And Interpretation Of Odds Ratio Or And Risk Ratio Rr Youtube

Incoming Term: odds versus probability, odds ratio versus probability, why use odds instead of probability, what is the difference between odds and probability, are odds and probability the same,